Reduced Order Observer Based Pole Placement Design for Inverted Pendulum on Cart

DOI:
https://doi.org/10.54060/JIEEE/003.02.002Keywords:
Inverted pendulum, Pole placement, State feedback, Reduced order, Euler-LagrangeAbstract
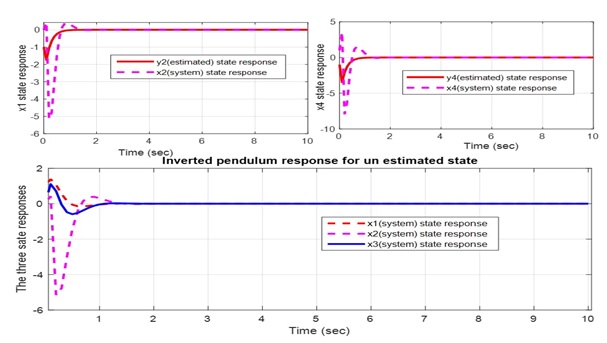
The inverted pendulum is an under actuated system and unstable system without a con-troller. In this paper modelling of an inverted pendulum is done using the Eu-ler-Lagrange equation for stabilization of it. The controller gain is evaluated through state feedback and reduced-order observer design techniques and the result for the dif-ferent initial conditions is compared. The state feedback controller is designed by Pole- placement technique for different desired pole locations. The simulation of the inverted pendulum based on reduced order pole placement design has been done on MATLAB/SIMULINK. It has been observed from the simulation result that the angular velocity and cart speed tracks the system response for different initial conditions by var-ying the desired pole location for the left-hand plane of the s-plane. In general, if some of the systems are unknown and the other state is known we can design using a re-duced-order observer for any physical system.
Downloads
References
A. J. Asuk, “feedback linearization, sliding mode and swing up control for the inverted pendulum on a cart,” Dissertation on Manchester University, 2015.
P. Kumar, O. N. Meharotra, J. Maheto, ““Controller design of inverted pendulum using pole placement and lqr,” Int. J. Res. Eng. Technol., vol. 01, no. 04, pp. 532–538, 2012.
K. Ogata, Modern Control Engineering: International Edition, 5th ed. Upper Saddle River, NJ: Pearson, 2010.
A. Rybovic, M. Priecinsky and M. Paskala, "Control of the inverted pendulum using state feedback control," 2012 ELEKTRO, 2012, pp. 145-148, doi: 10.1109/ELEKTRO.2012.6225627.
A. A. Roshdy, L. Yu zheng, H. F. Mokbel, and W. Tongyu, “Stabilization of real inverted pendulum using pole separation factor,” in Proceedings of the 1st International Conference on Mechanical Engineering and Material Science, 2012.
I. Siradjuddin, Z. Amalia, B. Setiawan, R. P. Wicaksono, and E. Yudaningtyas, “Stabilising a cart inverted pendulum system using pole placement control method,” in 2017 15th International Conference on Quality in Research (QiR) : International Sympo-sium on Electrical and Computer Engineering, 2017.
R. Banerjee and A. Pal, “Stabilization of inverted pendulum on cart based on pole placement and LQR,” in 2018 International Conference on Circuits and Systems in Digital Enterprise Technology (ICCSDET), 2018.
R. Bitirgen, M. Hancer, and I. Bayezit, “All stabilizing state feedback controller for inverted pendulum mechanism,” IFAC-Papers OnLine, vol. 51, no. 4, pp. 346–351, 2018.
V. Oguntosin, S. O. Oruma, A. Akindele, and A. Abdulkareem, “Control design of an inverted pendulum on a moving base using state feedback,” IOP Conf. Ser. Mater. Sci. Eng., vol. 1107, no. 1, p. 012064, 2021.
V. Suphatsatienkul, D. Banjerdpongchai and M. Wongsaisuwan, "Design of reduced-order observer and linear quadratic regu-lator for inverted pendulum on cart," 2017 56th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), 2017, pp. 1039-1044, doi: 10.23919/SICE.2017.8105752.
I. Siradjuddin et al., “State-feedback control with a full-state estimator for a cart-inverted pendulum system,” Int. j. eng. tech-nol., vol. 7, no. 4, pp. 203-211, 2018.
R. Nithya and C. Vivekanandan, “Stability Analysis and State Feedback Stabilization of Inverted Pendulum”, International Journal of Computer Science and Mobile Computing, Vol. 3 Iss. 5, pp. 310-320, 2014.
M. Fauziyah, Z. Amalia, I. Siradjuddin, D. Dewatama, R. P. Wicaksono, and E. Yudaningtyas, “Linear quadratic regulator and pole placement for stabilizing a cart inverted pendulum system,” Bull. Electr. Eng. Inform., vol. 9, no. 3, pp. 914–923, 2020.
I. Siradjuddin, Z. Amalia, B. Setiawan, R. P. Wicaksono, and E. Yudaningtyas, “Stabilising a cart inverted pendulum system using pole placement control method,” in 2017 15th International Conference on Quality in Research (QiR) : International Sympo-sium on Electrical and Computer Engineering, 2017.
K. K. Pramanik, S. Minz, “study of inverted pendulum using conventional and optimal controller,” International Journal of Elec-trical and Electronics Engineer, Vol. 9, Iss. 1, pp. 1819-1827, 2017.
L. Messikh, E.-H. Guechi, and S. Blažič, “Stabilization of the cart-inverted-pendulum system using state-feedback pole-independent MPC controllers,” Sensors (Basel), vol. 22, no. 1, p. 243, 2021.
M. Sharma and K. Pal, “Optimal Controller Design for Inverted Pendulum System: An Experimental Study”, International Journal of Scientific & Engineering Research, Vol. 11, Iss. 12, pp. i68-175, 2020.
A. U. Sambo, F. S. Bala, N. M. Tahir, and A. Y. Babawuro, “Optimal control of inverted pendulum on cart system,” J. Phys. Conf. Ser., vol. 1502, no. 012024, pp. 1-8 2020.
S. K. Mishra and D. Chandra, “Stabilization and tracking control of inverted pendulum using fractional order PID controllers,” J. Ind. Eng., vol. 2014, pp. 1–9, 2014.
S. Jung and J. T. Wen, “Nonlinear model predictive control for the swing-up of a rotary inverted pendulum,” J. Dyn. Syst. Meas. Control, vol. 126, no. 3, pp. 666–673, 2004.
L. B. Prasad, B. Tyagi, and H. O. Gupta, “Optimal control of nonlinear inverted pendulum system using PID controller and LQR: Performance analysis without and with disturbance input,” Int. J. Autom. Comput., vol. 11, no. 6, pp. 661–670, 2014.
Downloads
Published
How to Cite
CITATION COUNT
License
Copyright (c) 2022 Alemie Assefa

This work is licensed under a Creative Commons Attribution 4.0 International License.

























